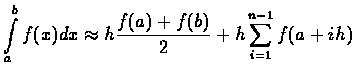
gdzie ![]() jest liczbą kroków całkowania a
jest liczbą kroków całkowania a ![]() .
Skompiluj i uruchom program dla funkcji zakodowanej w module funkcja.f
a=0, b=1 oraz 100 kroków całkowania. Sprawdź, czy program działa
poprawnie.
.
Skompiluj i uruchom program dla funkcji zakodowanej w module funkcja.f
a=0, b=1 oraz 100 kroków całkowania. Sprawdź, czy program działa
poprawnie.
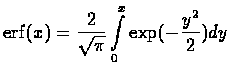
Tabelka powinna być wydrukowana w postaci sformatowanej.