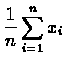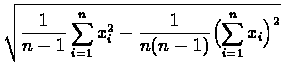Kurs MPI - pracownia nr 2

Celem ćwiczenia jest nabranie biegłości w posługiwaniu się procedurami komunikacji zbiorowej. Dokładny opis procedur komunikacji zbiorowej można znaleźć np. w rozdziale Collective communication książki MPI: The Complete Reference

Studenci i doktoranci: kody źródłowe oraz wydruk otrzymanych wyników (najlepiej w postaci tar.gz) proszę wysłać mailem na adres adam@chem.univ.gda.pl; będzie to sprawozdanie z tej pracowni. Przysłanie samego tekstu programu nie zalicza pracowni. Czas: do 10 kwietnia 2008.

Procedury MPI_BCAST, MPI_SCATTER i MPI_REDUCE

Napisać program obliczający średnią arytmetyczną $\overline{x}$oraz odchylenie standardowe s układu n punktów, pracujący na p procesorach. Wielkości te są zdefiniowane następującymi wzorami:

 

$$\overline{x} = \frac{1}{n}\sum_{i=1}^n x_i$$

$$\sigma = \sqrt{\frac{1}{n-1}\sum\limits_{i=1}^n x_i^2 - \frac{1}{n(n-1)}\bigl(\sum\limits_{i=1}^n x_i\bigr)^2}$$

Procesor 0 czyta wszystkie dane (liczbę punktów oraz współrzędne wektora x) a następnie rozsyła do każdego procesora liczbę punktów n (procedura MPI_BCAST) oraz tylko tę część, która jest procesorowi potrzebna do obliczenia jego części sumy (procedura MPI_SCATTER lub MPI_SCATTERV). Procesory liczą swoje części sum $\sum\limits_{i=1}^n x_i$oraz $\sum\limits_{i=1}^n x_i^2$, po czym sumy całkowite są zbierane przez procesor 0 (MPI_REDUCE).

Dla ułatwienia początkowo założyć, że liczba punktów jest podzielna przez liczbę procesorów, następnie uwzględnić przypadek ogólny, przy czym należy zadbać o jak najrówniejszy podział punktów pomiędzy procesory (load balancing).