Kurs MPI - pracownia nr 4
Uwaga: studenci i doktoranci pragnący uzyskać zaliczenia z przedmiotu przoszeni są o nadesłanie rozwiązań na adres adam@chem.univ.gda.pl do dnia 19 maja 2008.
Celem ćwiczenia jest zapoznanie się z uruchamianiem zadań równoległych na klastrze holk.task.gda.pl w CI TASK, zarówno interaktywnie, jak i pod systemem kolejkowania PBS. Należy zwrócić uwagę, że zadania interaktywne mogą być jedynie bardzo krótkie i zużywać bardzo niewiele zasobów. Większe zadania, szczególnie obliczenia produkcyjne należy uruchamiać pod systemem PBS.
Przed przystąpieniem do rozwiązywania zadań proszę się zalogować najpierw na komputer kdm.task.gda.pl (serwer karawela) a nasętpnie holk.task.gda.pl. Z katalogu ~adaml proszę skopiować na swój katalog domowy podkatalog MPI/plastocyanin.
1. Kompilacja
programów równoległych oraz uruchamianie zadań na
holku w CI TASK
Skopiować program hello.c lub hello.f z pracowni
touch ~/.mpd.conf
Na klastrze holk nie uruchamia się zadań interaktywnych. Dlatego należu uruchomić program hello pod systemem kolejkowania PBS wykorzystując skrypt run.sub, który jest w katalogu ~adaml/MPI/Cw1/C oraz ~adaml/MPI/Cw1/F77. Wprowadzić zadanie do systemu kolejkowania poleceniem:
qsub run.sub
Ponieważ klaster holk jest mocno obciążony, zadanie zapewne nie wystartuje od razu. Przewidywany czas startu zadania można sprawdzić poleceniem
showstart nr_zadania
Liczbę procesorów oraz czas specyfikuje się w skrypcie w linii:
#PBS –l nodes=xx:ppn=yy,walltime=HH:MM:SS
Liczba procesorów=xx*yy; ponieważ nody są 4-procesorowe dla liczby procesorów>4 zaleca się użycie całkowitej wielokrotności 4.
Ponieważ wydruk wyniku jest na stdout, pokaże się on w pliku run.sub.oxxxxxx gdzie xxxxxx jest numerem zadania.
2.
Przykładowe obliczenia programem AMBER: dynamika molekularna
Zawarty w tym ćwiczeniu przykład dotyczy pakietu mechaniki i dynamiki molekularnej AMBER. Są to krótkie (2 ps) obliczenia dynamiki molekularnej plastocyjaniny wykonywane przy użyciu modułu sander pakietu.
Przykładowe skrypty do uruchamiania zadań pod PBS znajdują się w /apl/pbs/examples . Skrypt do uruchamiania programu sander znajduje się w ~adaml/MPI/plastocyanin/run.csh.
Uruchomić skrypt run.csh na jednym, 1, 2, 4, 8 i 16
procesorach pod systemem kolejkowania PBS. Dla 8 i 16 procesorów należy
zaspecyfikować odpowiednio nodes=2:ppn=4 i
nodes=4:ppn=4 w skrypcie run.csh. Można wykorzystać kolejkę test,
która jest przeznaczona do krótkich zadań do 16 procesorów i ma najwyższy
priorytet ale lepiej użyć kolejki test. Na końcu pliku plc.out
jest podany rzeczywisty czas wykonania zadania (Nonsetup wallclock);
można tam też znaleźć jego podzial na czas zyżyty na
wykonanie poszczególnych modułów programu. Zwrócić uwagę na czas zużyty dla
obliczeń oddziaływań niewiążących (Nonbond); jest ich w przybliżeniu ![]() , gdzie
, gdzie ![]() jest liczbą atomów) a zatem czas zużyty na ich
obliczenie to gros wysiłku obliczeniowego oraz na czas zużyty na sumowanie
energii, co zawiera również w sobie przesyłanie komponentów energii (FRCSUM).
Pełniejszą analizę czasów wykonania poszczególnych modułów programu z
rozpisaniem na poszczególne procesory można znaleźć w
pliku logfile.
jest liczbą atomów) a zatem czas zużyty na ich
obliczenie to gros wysiłku obliczeniowego oraz na czas zużyty na sumowanie
energii, co zawiera również w sobie przesyłanie komponentów energii (FRCSUM).
Pełniejszą analizę czasów wykonania poszczególnych modułów programu z
rozpisaniem na poszczególne procesory można znaleźć w
pliku logfile.
3. Analiza skalowalności: prawo Amdahla
Przeprowadzić analizę czasu obliczeń dynamiki molekularnej z punktu 2.1 w
zależności od liczby użytych procesorów. Wyjaśnić zaobserwowaną zależność. Wykonać wykres zależności
przyspieszenia obliczeń od liczby procesorów oraz
wydajności obliczeń od liczby procesorów. Wielkości te
są zdefiniowane następująco:
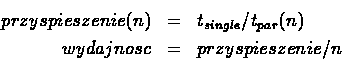
gdzie ![]() jest liczbą procesorów,
jest liczbą procesorów, ![]() jest czasem wykonania zadania na pojedynczym
procesorze a
jest czasem wykonania zadania na pojedynczym
procesorze a ![]() jest czasem
wykonania zadania na
jest czasem
wykonania zadania na ![]() procesorach.
procesorach.
Dopasować otrzymaną zależnośc do teoretycznej zależności danej przez prawo Amdahla i wyliczyć ułamek czasu obliczeniowego, który odpowiada niezrównoleglalnej części kodu?